Introduction
Recently, I’ve been tutoring for the SAT, and I noticed one of my students was struggling with some of the SAT math questions. More specifically, they were struggling with Right Triangle Trigonometry questions. Now, I don’t blame them. In my opinion, these are some of the hardest questions that the SAT tests you on. Because of their relatively high difficulty compared to other questions, I felt it was appropriate to address an example of how I’d go about solving one in a blog post.
Understanding The Problem
Let’s take a look at the problem that this student was struggling with.
(Note: If you think you’ve already got a good understanding of trigonometry and just want to see the solution, you can skip ahead to “Solving the Problem.”)

The question reads: “Side length t is 6.43 and s is 5.39. Given that s / t ≈ tan(0.697) ≈ sin(0.994) ≈ cos(0.576), approximately what is the measure of angle β in radians, to the nearest tenth?”
Looks pretty difficult, right? I took this problem straight from Khan Academy’s SAT prep questions. At first glance, you may have no idea how to solve it. Let’s try and break it down, though, to get a better understanding of what we’re working with here.
It’s clear that the question is asking us to find the measure of the angle β (Beta), but the method we’re supposed to use isn’t readily apparent. The only other information that’s given is that the ratio of the two sides, s / t, is equal to some angles plugged into some trigonometric functions.
The fact that s / t is equal to tan(0.697) and all those other trig values may seem completely abstract, but there’s actually an easy way to conceptualize it. If you recall SOHCAHTOA and your trig/inverse trig relationships…
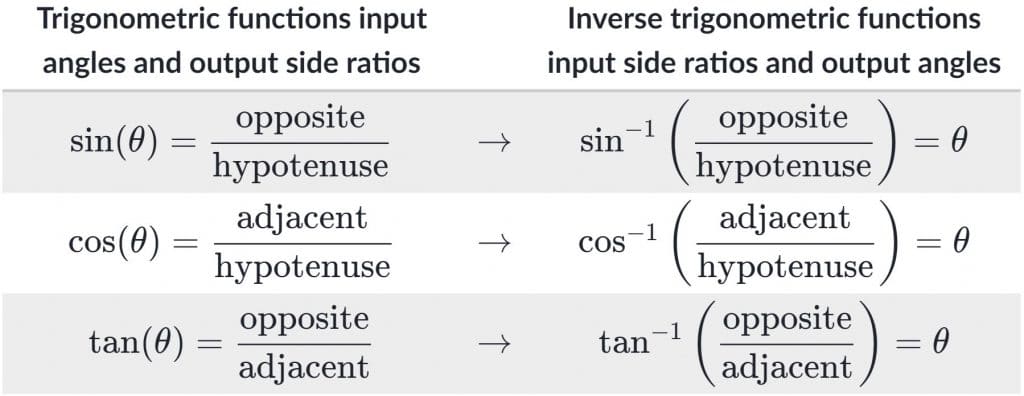
…it simply means that when a triangle is formed with side length s on the opposite side of an angle, and side length t on the hypotenuse of that triangle, then that angle will be 0.994 radians. Hence the s / t = sin(0.994)
Likewise, if a triangle is formed with side length s on the adjacent side of an angle, and side length t on the hypotenuse of that triangle, then that angle will be 0.576 radians. Hence the s / t = cos(0.576)
Finally, if a triangle is formed with side length s on the opposite side of an angle, and side length t on the adjacent side of that angle, then that angle will be 0.697 radians. Hence the s / t = tan(0.697).
If you’re still confused as to what that might look like, here’s a visualization I created to help you understand:
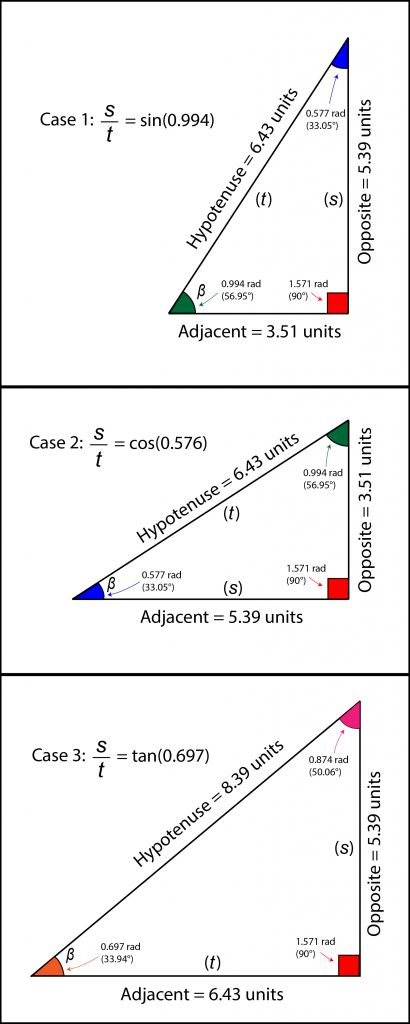
In our case, since the angles are changing but the sides being referenced are not, our chart would look a little more like this:
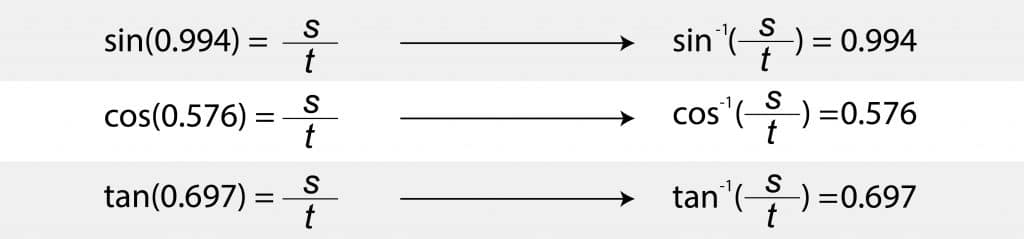
By using all of the information in the chart above, we can actually try to get β in place of one of these angles (i.e., replace either 0.994, 0.576, or 0.697 with β). This means we must encounter one of three situations in the problem:
- The side OPPOSITE angle β is s, and the HYPOTENUSE is t.
- The side ADJACENT angle β is s, and the HYPOTENUSE is t.
- The side OPPOSITE angle β is s, and the side ADJACENT to angle β is t.
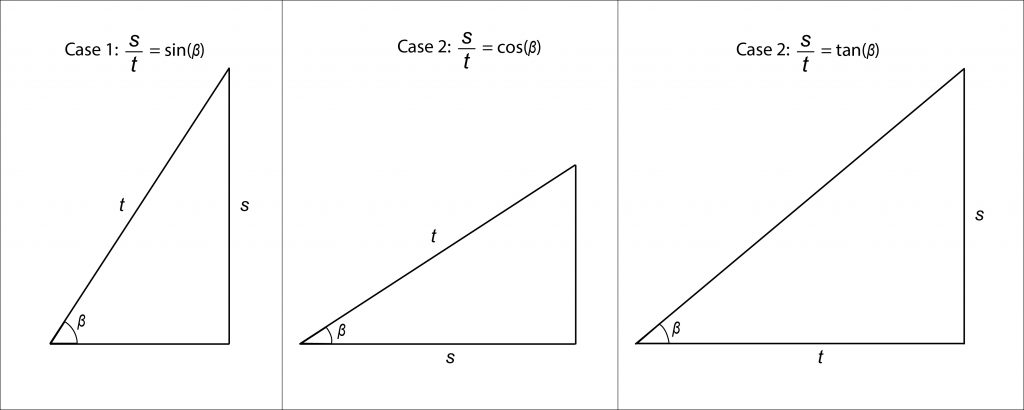
By definition, if we can get β into one of these three positions, then we already have our answer, since the trig relationships for three angles are already defined in the question. Since we’re given three angles to choose from (0.697, 0.994, and 0.576), we could also make a guess here and have a 33% chance of getting it right, but let’s see how we can solve the problem.
Solving the Problem
Now that we know what we’re looking for, we can go ahead and try to get β, s, and t together in a way that allows us to solve the problem. Believe it or not, we actually have all the information we need to solve this problem. By filling in missing information based on what we already know, we can make this problem a little bit easier to solve.
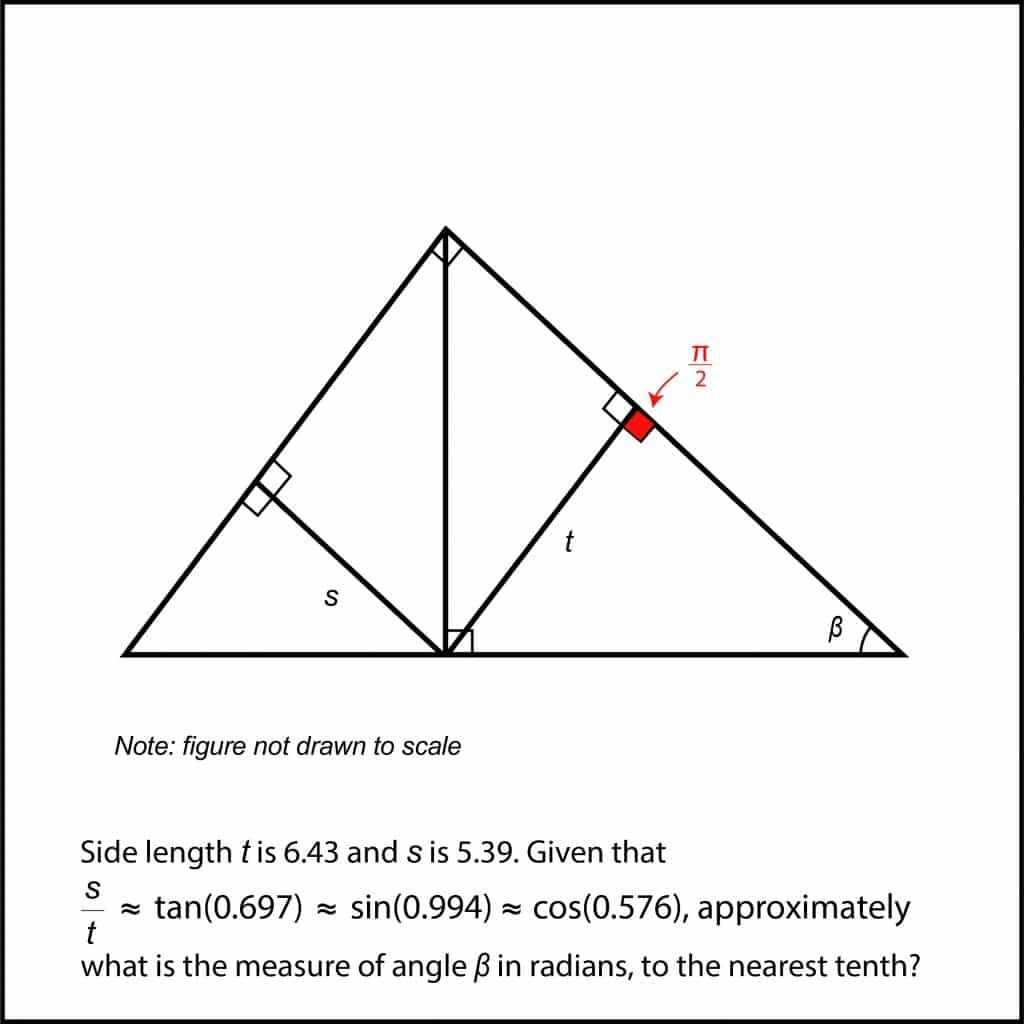
First, note that the small triangle containing β contains a right angle. We’ll label this angle as π / 2, since we’re working in radians, but it’s also equivalent to 90 degrees.
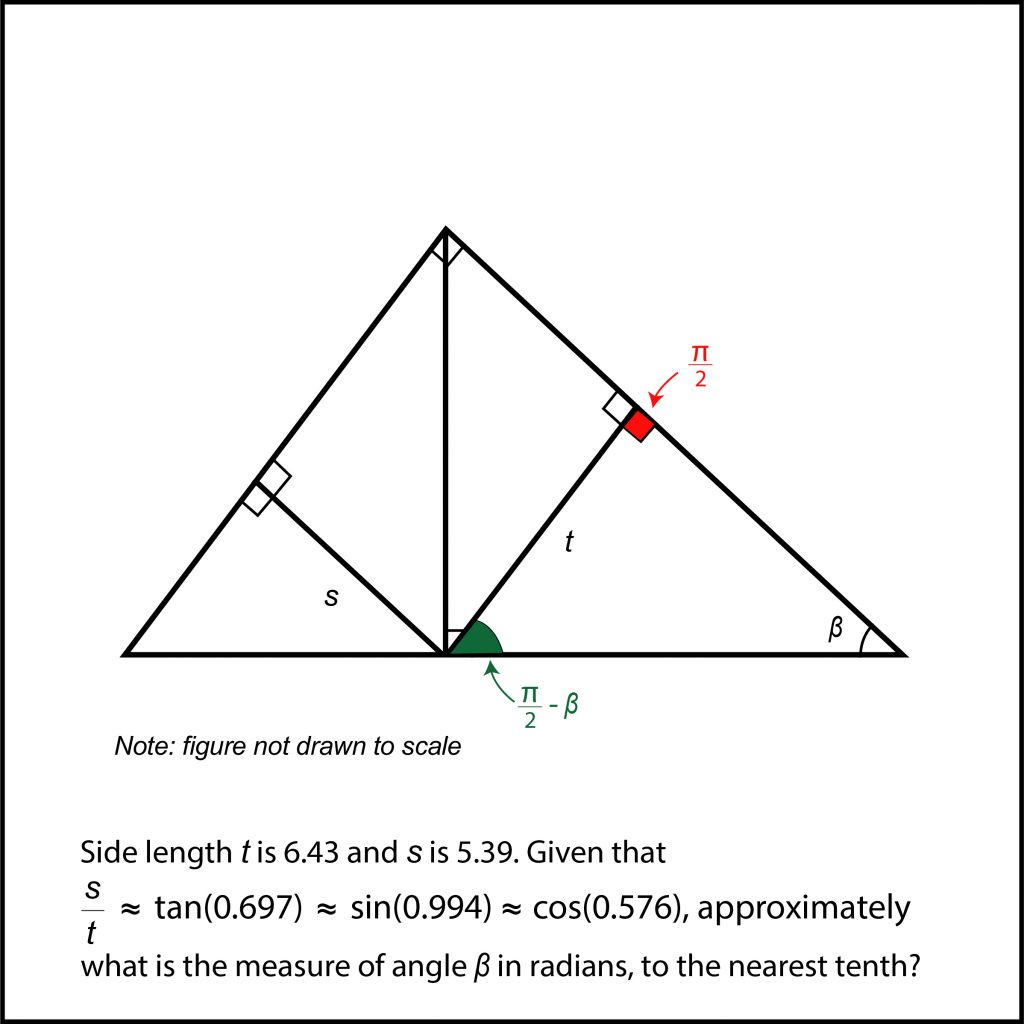
Next, we’ll label the last angle of this triangle as (π / 2) – β. We’ll do this because we don’t yet know the measure of this angle, but since we know the measure of the other two angles, we can write the last one in terms of the first two. Since all angles in a triangle add up to 180°, or π, the remaining angle is π – (π / 2) – β = (π / 2) – β.
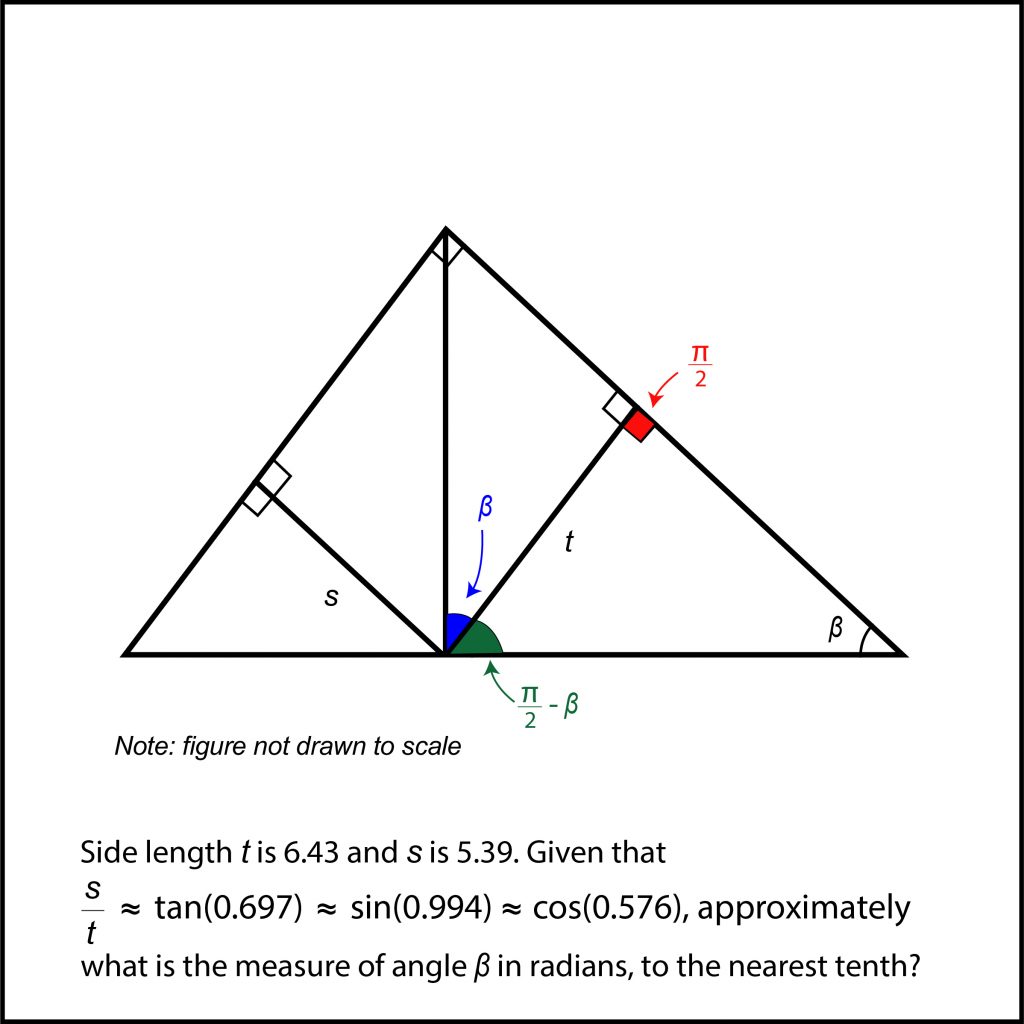
Now that we have those three angles, we can begin labeling the angles of some of the other triangles. Since we know that the vertical line forms a right angle (90°) with the base of the largest triangle, we know that the two angles formed by the diagonal line (between the blue and green sections) are complementary. This means that they will add to 90°, or π / 2. That means that the blue angle is equal to π / 2 – (π / 2 – β), or simply β.
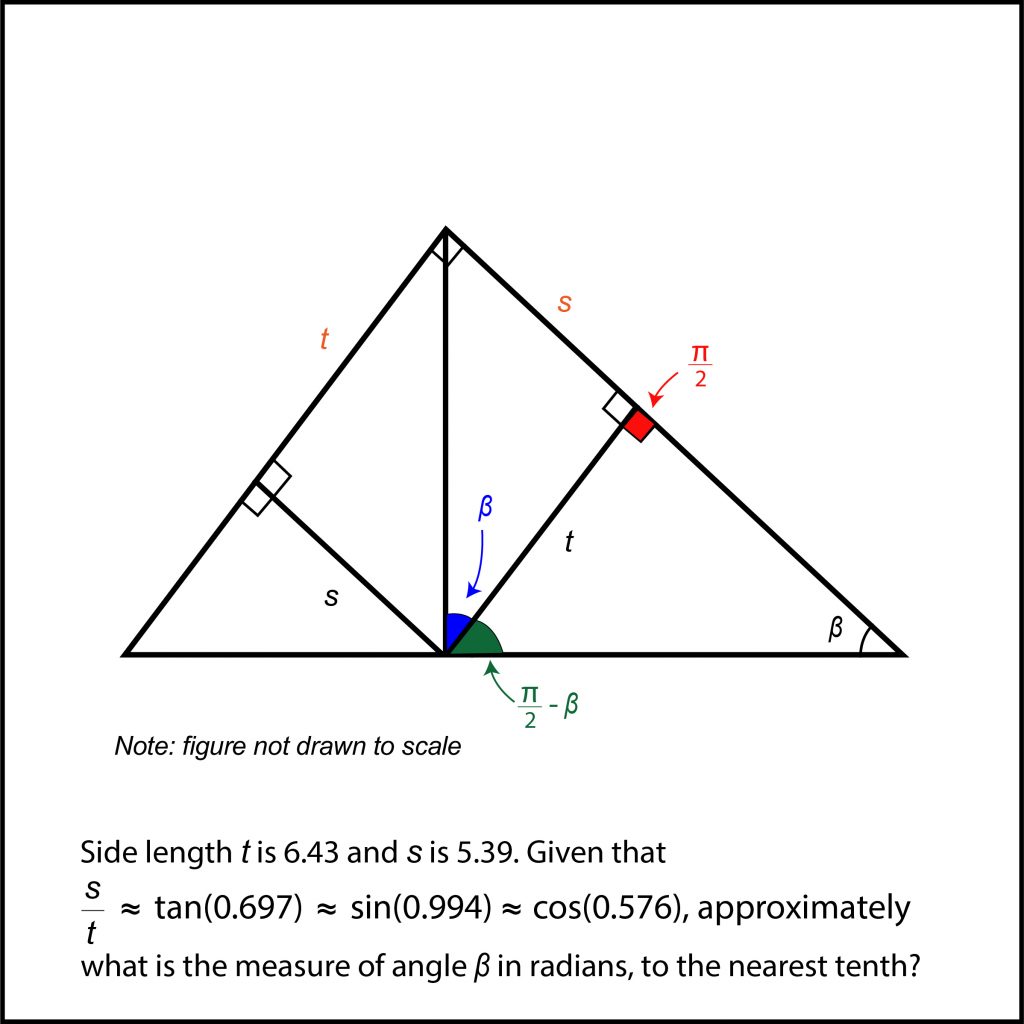
From here, we can begin to incorporate s and t into the picture. Note that the quadrilateral formed between s and t has three right angles, which means that the last angle must also be a right angle. This follows directly from the fact that a quadrilateral has four angles that add up to 360°. Because of this, we know that each pair of opposite sides are equal in length, and we can label the remaining sides of the shape with s and t.
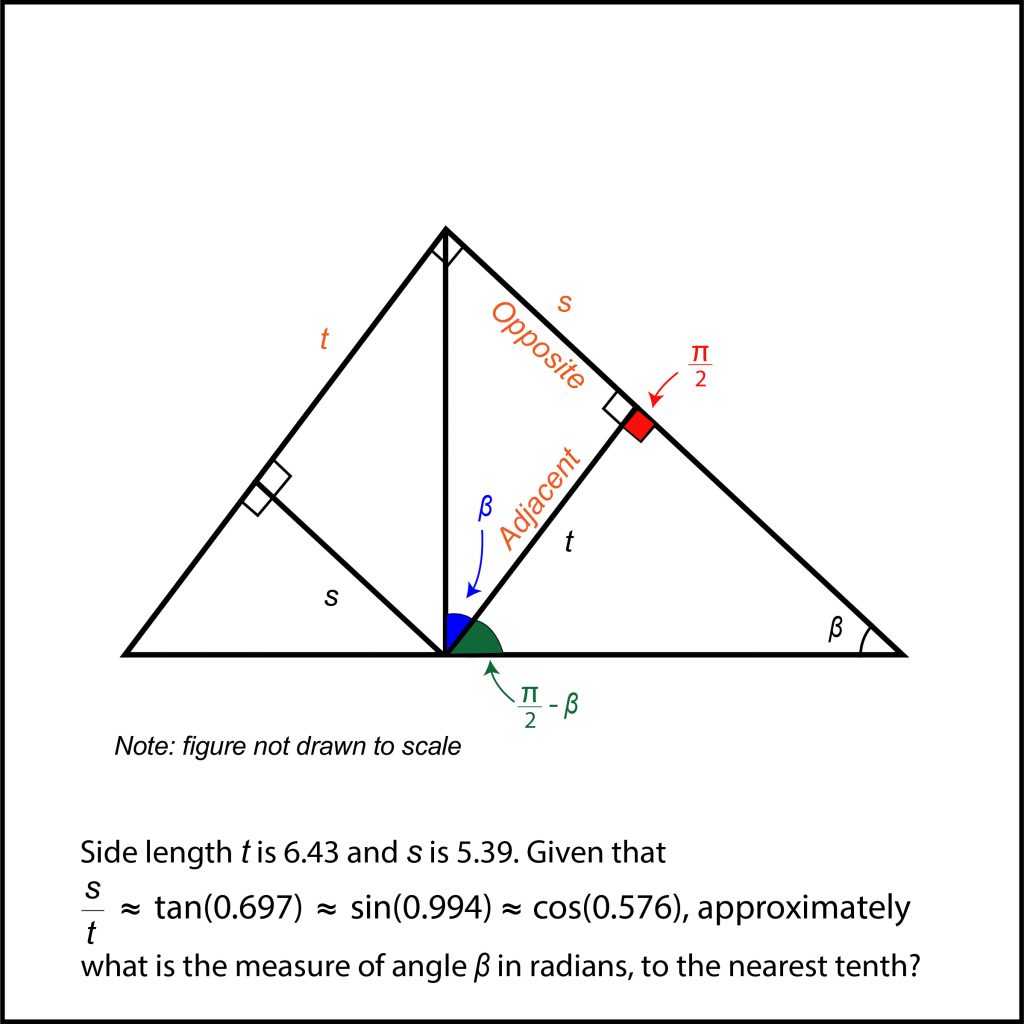
At this point you may start to see where the answer becomes apparent. Since we have β, s, and t together, we can label the sides according to their position relative to β. I didn’t label the hypotenuse because it wasn’t relevant to this particular situation, but if the hypotenuse was s or t then I would have labelled it as well. Now that we have our sides’ relations to the angle β, we can use the original information given to solve the question.
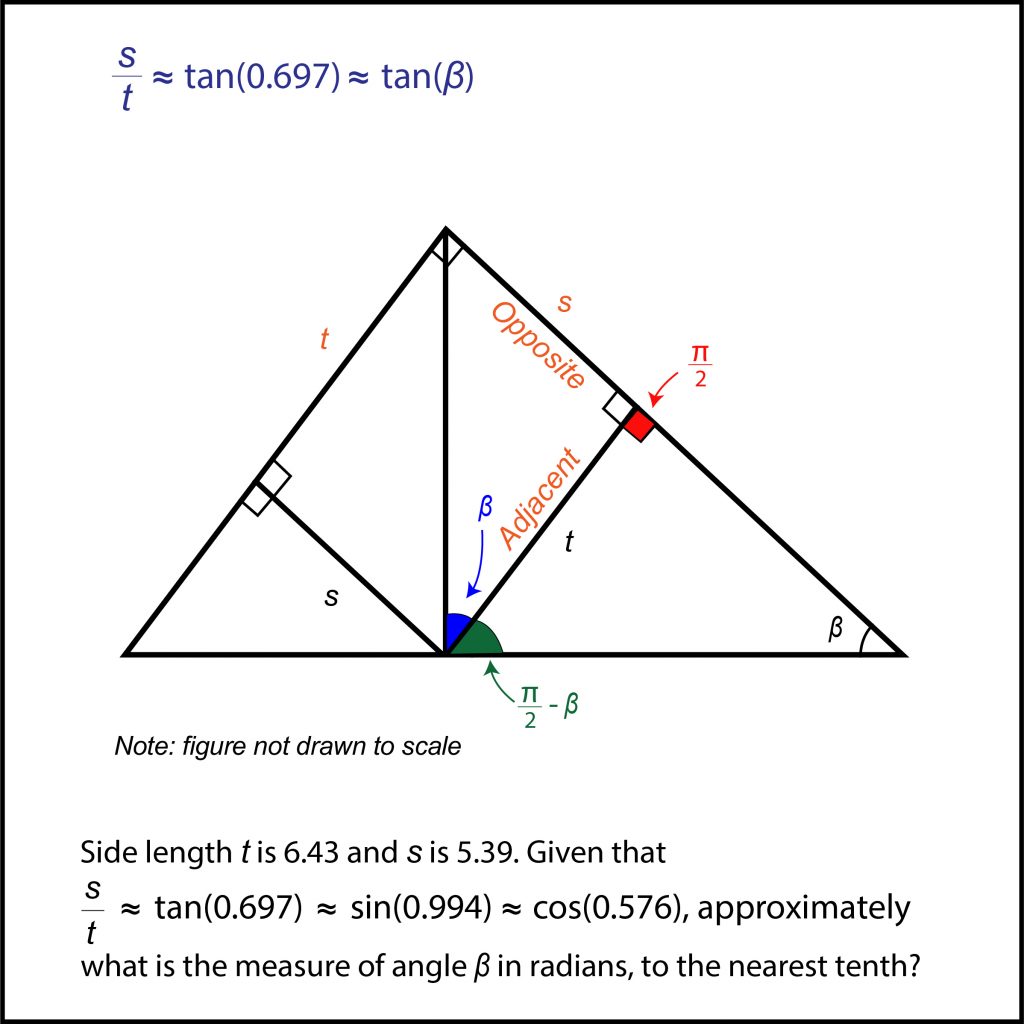
Since the two sides with s and t were the opposite and the adjacent sides to the angle, we’ll be using a tangent relationship to finish up this problem. We can set up the relation given to us from the problem, where the ratio of the two sides, s / t, is the tangent of the angle 0.697. In this case, it is the tangent of the angle β as well!
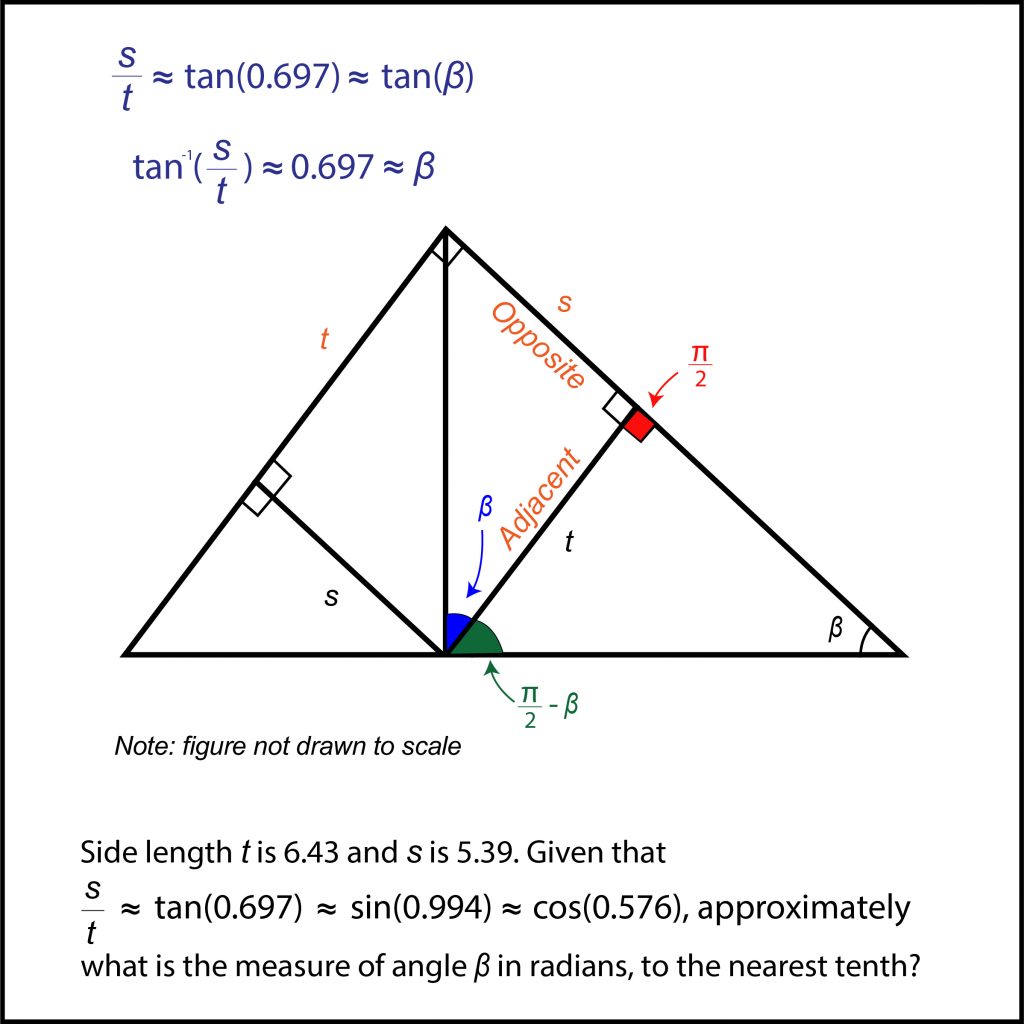
By now you can probably see that β is equal to 0.697. However, if you want to go one step further and do it properly, you’d take the inverse tangent of both sides of the equation. This will show you that the inverse tangent of (s / t) is equal to 0.697 radians, which is equal to the angle β.
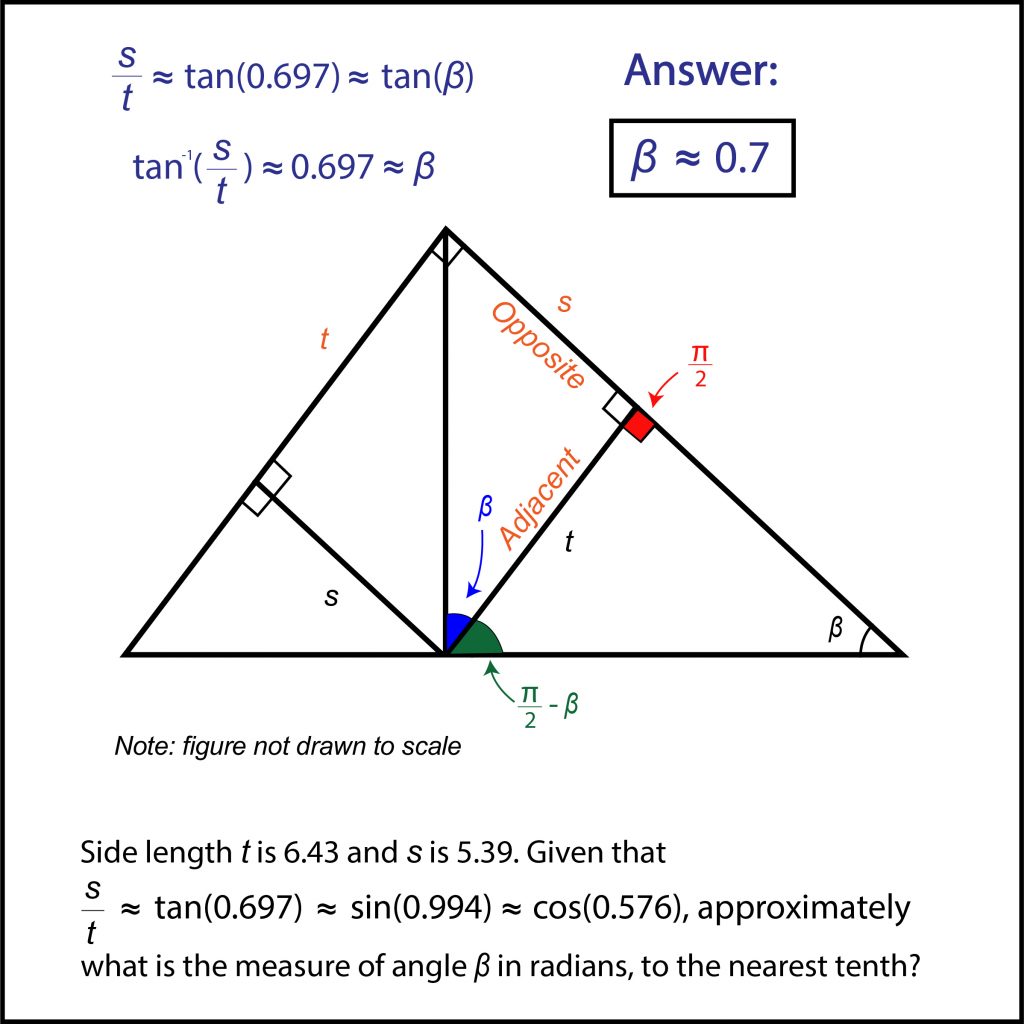
And so we arrive at our answer: 0.7 radians. Make sure you pay attention to the wording of the question and round the answer to the nearest tenth, otherwise it would be marked wrong on the SAT!
Summary (Tips and Tricks)
The biggest takeaway from this example should be that as long as you have the necessary knowledge, any problem on the SAT is manageable when you break it down. (If you’re missing some content knowledge, though, I’d recommend you go and learn those concepts first).
The process I use generally goes as follows:
- Try to figure out what exactly the question is asking you. In this case, it was pretty clearly stated what the question was looking for. However, it took a bit of thinking to determine how to arrive at such an answer, and what the other information given in the question meant.
- Figure out what information is relevant and how it’s relevant. In this problem, we knew that we’d be using the trigonometric relationships given to solve for the angle β. We knew that we had to relate β, s, and t somehow to arrive at our answer.
- Use what you’re given to fill in missing information and solve. In this problem, all the information we needed was given, but not everything was explicitly written on the figure. We had to fill in certain angles and side lengths by logical reasoning as well as implementing some geometry/trigonometry rules.
I hope that you found this post helpful for your SAT prep journey, and hopefully it makes you better with solving right triangle trigonometry questions on the SAT. If anything I wrote was unclear, just let me know and I’ll try to clarify it. Keep on practicing!
6 Comments
Mahad Khan · June 18, 2020 at 9:27 PM
Very well explained
Trish · January 2, 2021 at 5:16 PM
thanks for the explaination, it really helped me a lot!
Matthew · April 5, 2021 at 3:55 AM
I was on khan academy and usually, they are pretty good at explaining the question but this time I was left so confused, Thank you for clearing that up
Asal · July 19, 2023 at 12:34 AM
Thank you for the explanation
Burt · February 3, 2024 at 1:33 AM
I think case 3 angle should be 39— instread of 33—
Dan · April 10, 2024 at 12:33 AM
You’re so right Burt. Thanks for the catch 🙂