The Problem in Question

Recently, I posted a video on TikTok (@danstestprep) showing how you can save valuable time on the SAT Math section.

The video did quite well, and I assume it was because I solved a very difficult-looking problem in just two seconds. The question I covered dealt with complex fractions, and you can take a look at it below:

Basically, I was able to recognize that whenever you have a fraction in this form, the answer is always going to be the quadratic expression over the linear expression. In this case, that corresponds to answer choice C.

But why exactly does this work, and when can you use this trick?

Keep reading, because I’m going to show you the specific cases in which you can use this trick, as well as one simple method that you can use to solve any complex fraction questions.

The Time-Saving Trick

Before we begin, there are some terms you need to know.

Remember that a quadratic term is a term where the highest power on the variable is a 2. This can typically be seen as an x² term.

A linear term is simply a term where the highest power on the variable is a 1. This is typically seen as an x¹ term, or simply an x (the exponent of 1 is implied).

A constant term is just a term without any variables; therefore its value cannot change.

Let’s begin by analyzing the way our problem is set up. Notice that we have a complex fraction where there is a constant in the numerator, and then the addition of two fractions in the denominator. The fractions nested in the denominator are formatted so that there is a constant in their numerators and a linear term in their denominators.

If you’re confused, here’s an image of what I mean by all that:

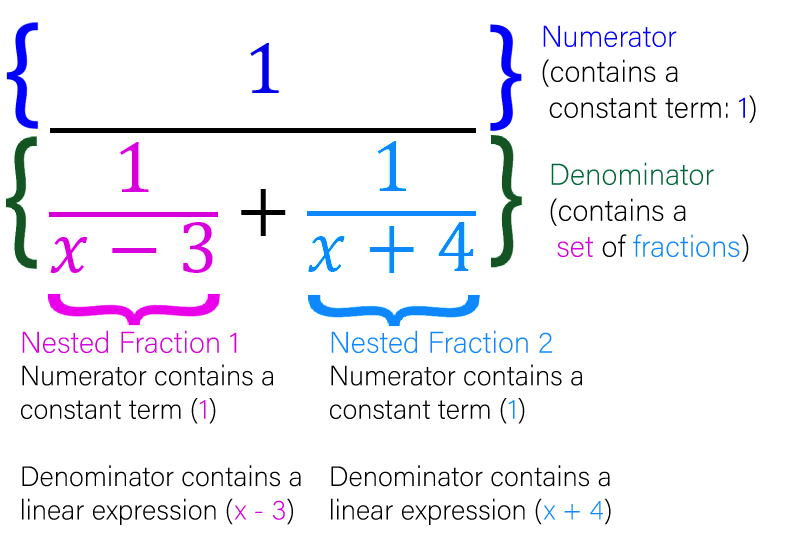
This trick can only be used under the following conditions:

1. The numerator has to be a constant (does not necessarily have to be a 1)
2. The denominator must contain two fractions (either being added or subtracted, it doesn’t matter)
   • These fractions must have a constant in their numerators (again, can be any constant) and a linear expression in their denominators. This linear expression must be a BINOMIAL, meaning it has two pieces (an x term and a constant).

If these conditions are met, then your answer will simply be the choice with the quadratic expression over the linear expression. That’s really all there is to this trick.

In the next section, I’ll show you why this works, and how you can solve ANY complex fraction problem by just breaking it down.

Solving the Problem, Algebraically

While solving a question in two seconds would certainly be useful on the SAT, it’s not always feasible to do so. The problem may be presented in a different format or context, requiring you to simplify the complex fractions. I’ll be teaching you exactly how you can tackle those complex fractions no matter where they show up.

Let’s start by taking a look at the expression in our original question:

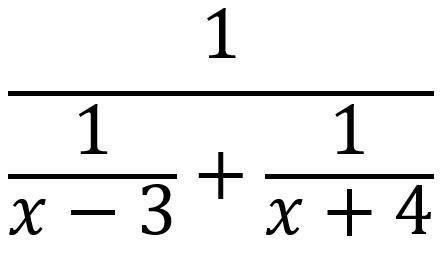
From here, I suggest that you find the common denominator of all the terms in the complex fraction. The easiest way to do this, in my opinion, is to just take the denominators of each term and multiply them together. The three denominators from our three terms are 1 (from 1/1), x – 3 (from 1/(x – 3)), and x + 4 (from 1/(x + 4)).

We can multiply these three expressions together to get our common denominator: (x – 3) · (x + 4). We could FOIL this out, but I’d like to keep it in this form for now.

Now that we have our common denominator, we can multiply it to both the top and bottom of our fraction:

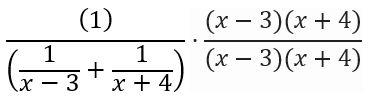
Make sure you multiply to BOTH the top and the bottom, because otherwise you’d be changing the value of the expression. By multiplying it to both the top and bottom, you’re essentially “multiplying by 1” since (x – 3)(x + 4) divided by itself is equivalent to 1.

Now if we distribute the fraction on the right into our expression, we end up with something that looks like this:

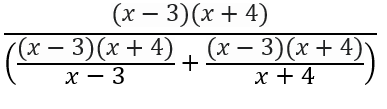
This looks very complex, but it really isn’t. Notice how we can cancel out the (x – 3)’s from the complex fraction on the left. Similarly, we can cancel the (x + 4) terms from the complex fraction on the right. This leaves us with something that looks like this:

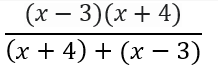
This is already looking a LOT simpler. From here, all you have to do is multiply the two terms in the numerator (I like to use FOIL) and add like terms in the denominator. This gives you your final result:

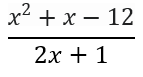
After all that work, you’re left with a quadratic term over a linear term, which is the same result that we got when using the two-second trick above.

By using this method of solving algebraically, you’ll be able to tackle ANY complex fraction!